This is a series of articles. All parts:
Let’s recap what we’ve learned so far about Semigroups:
- Semigroup is a type and a binary associative operation on values of this type.
- Quite a lot of things are semigroups: numbers with addition, booleans, string concatenation, min, max, lists, first, last.
- We can combine different semigroups in pairs.
We’ve looked mostly on trivial semigroup examples but before exploring more advanced and real-life use cases, I’d like to spend more time on exploring why associativity matters.
We’ll see how this single concept enables:
- Correctness
- Extensibility
- Performance
Example 1: Lists of Chunks
In the previous part, we’ve looked at the first real-world example of non-trivial Semigroup: a list of chunks with the overall size of element inside.
To remind, here’s the OCaml code:
(* --- line.ml --- *)
type t = {
chunks : Chunk.t list;
length : int;
}
let append line1 line2 =
let chunks = line1.chunks @ line2.chunks in
let length = line1.length + line2.length in
{ chunks; length }I use values of this type in my GitHub TUI project to append formatted strings and eventually output them to the terminal.
Efficient terminal rendering is quite a dirty business. A terminal screen is a mutable 2D-array of bytes. But I don’t have an array of bytes! I have chunks!
In other words, if I have three renderable parts line1,
line2, line3, I want to output them one after
another in this exact order.
Having a code like this:
append (append line1 line2) line3I expect the final rendered result to look like this:

You know, it would be a real shame, if I append these three lines like this:
append line1 (append line2 line3)And suddenly it renders like this:

If you ask me, how this could happen, I answer, “Pretty easy, in fact”. If you’ve never heard the phrase “premature optimisation is the root of all evil”, this is the time.
Imagine a function append that instead of appending two
lines, outputs them to a mutable buffer directly. If you do things like
this, you’ll get the demonstrated wrong behaviour.
In my GitHub TUI project, I append quite a lot of strings, and keeping track of their order will quickly become an impossible task that destroys all the productivity.
However, if I follow associative composable abstractions (which are quite simple in this case), I’ll get a design correct by construction.
🧑🔬 In the future parts, we’ll see how to use Semigroup to implement a blazingly fast mutable string builder abstractions (wat?).
Example 2: Treap
Let’s talk about associativity a bit more on the example of a classic Computer Science Data Structure known as treap.
I’m not going to explain it here, you can read about it on the Internet. I’ll just say that it’s a combination of tree and heap (hence the name).
Treap is a binary search tree over keys and a max-heap over randomly generated numbers.
We’ll look into special case of this data structure — treap with implicit keys. Here keys are indexes in the array.
To reduce the confusion a bit, let me give an example.
Imagine an array of values like this one:
Array: [5, 2, 1, 3, 2]Every element of this array has an index in the 0-based index system:
Array: [5, 2, 1, 3, 2]
Index: 0 1 2 3 4Now, let’s also generate a random number from 0 to 9 for every element:
Array: [5, 2, 1, 3, 2]
Index: 0 1 2 3 4
Random: 6 4 9 7 1A treap with implicit keys will represent a dictionary-like data structure, where:
- Indexes are keys
- Array values are our dictionary values
- Indexes (aka keys) form a Binary Search Tree
- Random values form a max-heap
Visualised, it looks like this:
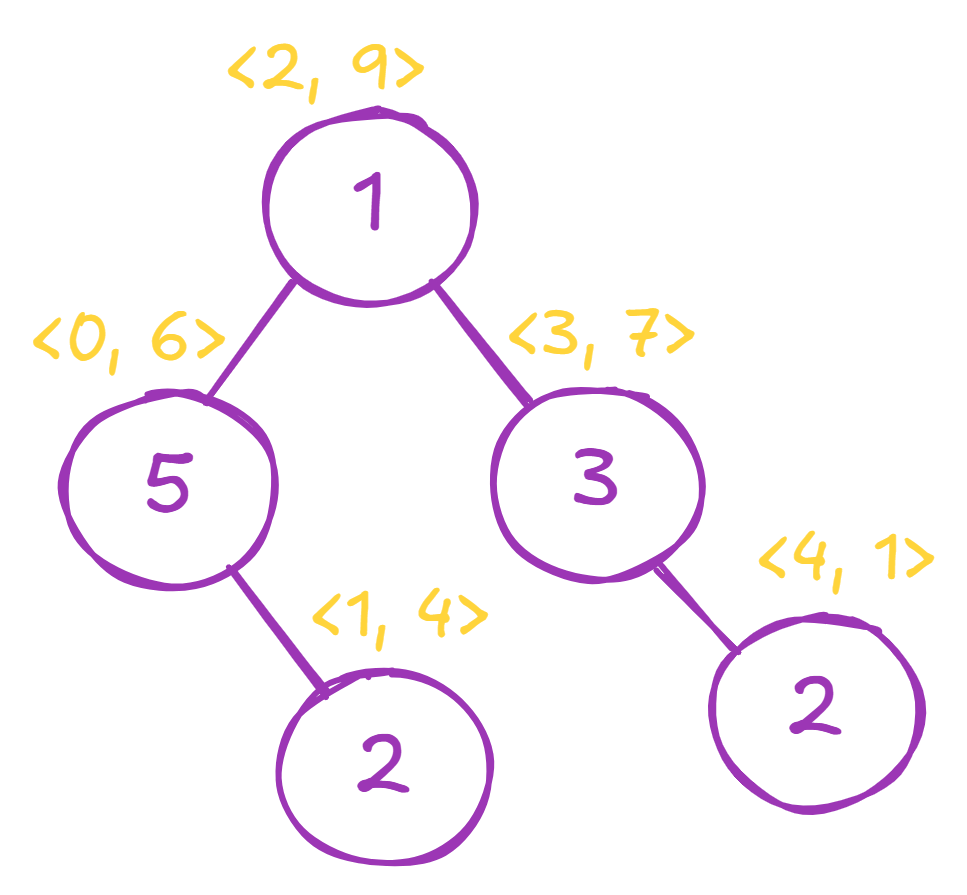
🧑🔬 Another name for treap is Cartesian Tree. You can think of keys as x-axis coordinates, and random values as y-axis coordinates for the tree node.
This may sound like a lot of overengineering, but in practice, it’s a quite clever data structure. Think of it as an array on steroids. It supports the following operations efficiently:
| Operation | Complexity |
|---|---|
| get | O(log n) |
| insert | O(log n) |
| delete | O(log n) |
| merge | O(log n) |
| reverse | O(log n) |
| slice | O(log n) |
| Binary associative operation | O(log n) |
What’s that last one? You guessed correctly, it’s our old friend smoosh.
Turns out, if treap values form a Semigroup, you can query the result of the Semigroup operation over any segment between two indexes. Moreover, the root of the treap will contain the result of this operation over all alements. So you have O(1) access to some operation over all elements.
To give an example,
| Binary Associative Operation | Root |
|---|---|
| Addition | Sum of all values |
| Multiplication | Product of all values |
| Max | The largest value |
| Min | The smallest value |
| First | Element with index 0 |
| Last | Element with index len - 1 |
In fact, why not have everything at the same time???
From the previous part we know that a pair forms a Semigroup where the binary associative operations for each part of the pair are applied correspondingly and indepedently (some might even say in parallel).
If we can construct a pair, we can have a triple.
We can have 7 elements.
We can have 15 elements.
To generalise, any record where every field is a Semigroup, automatically becomes a Semigroup itself.
It means, based just on this absraction of Semigroup, we’ve built an extensible interface where users just need to configure what they want to be calculated, and they automatically get an ability to query this operation over segments.
In competitive programming this technique becomes even more powerful,
because you can be creative with the Semigroup operation. For example,
you can calculate the number of elements equal to 0 in the entire treap
(yes, this is a Semigroup too!) automatically after every
insert and delete.
This example gives quite a visual explanation of associativity.
Imagine an array of three elements (it doesn’t matter what’s inside, so let’s give elements generic names):
Array: [x, y, z]
Index: 0 1 2If we want to calculate some binary operation (again, doesn’t matter which one, let’s just call it ⊕) over these elements, aka:
x ⊕ y ⊕ zthe shape of our Treap shouldn’t matter. It doesn’t matter, right? Let’s see.
Treap relies on generating random values. As long as those values are random, operations will be efficient. But the shape of the treap could be different.
If we have random values like this:
Array: [x, y, z]
Index: 0 1 2
Random: 5 3 9We’ll get the following treap:
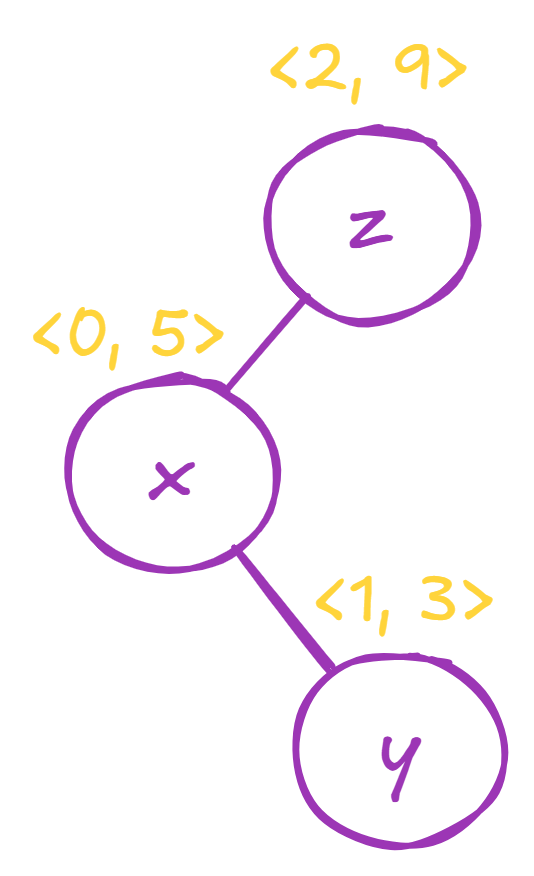
And the root will contain the result of:
(x ⊕ y) ⊕ zBut if random values are slightly different:
Array: [x, y, z]
Index: 0 1 2
Random: 9 3 5We’ll get a different treap
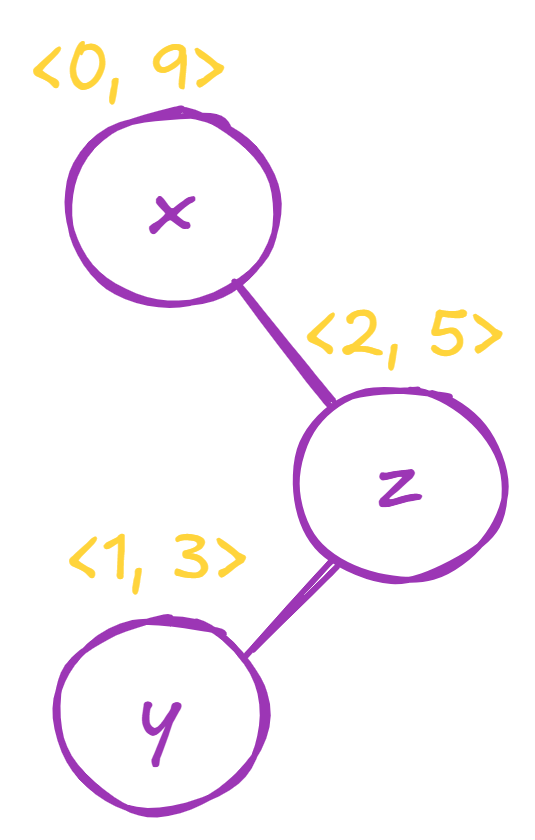
And the root will instead contain:
x ⊕ (y ⊕ z)We don’t want these two results be different. And they won’t be if our operation ⊕ is associative.
That’s why Semigroup is important here. We don’t need to care about internal implementation details as long as we provide the correct interface.
Who would’ve thought the OOP principle of encapsulation and separating internals from the interface would haunt us here??
In fact, the technique of calculating an associative binary operation over tree values can (and has been) successfully extended to other tree-like data structures e.g. Balanced Binary Search Tree, Segment Tree, or Finger Tree.
Want to hear the coolest part?
Treap itself is a Semigroup with the binary associative operation being the merging of two treaps. It also automatically calculates the final result efficiently 🤯
I’ll leave you with this.
Example 3: MapReduce
Let’s take a step back and look at a different example.
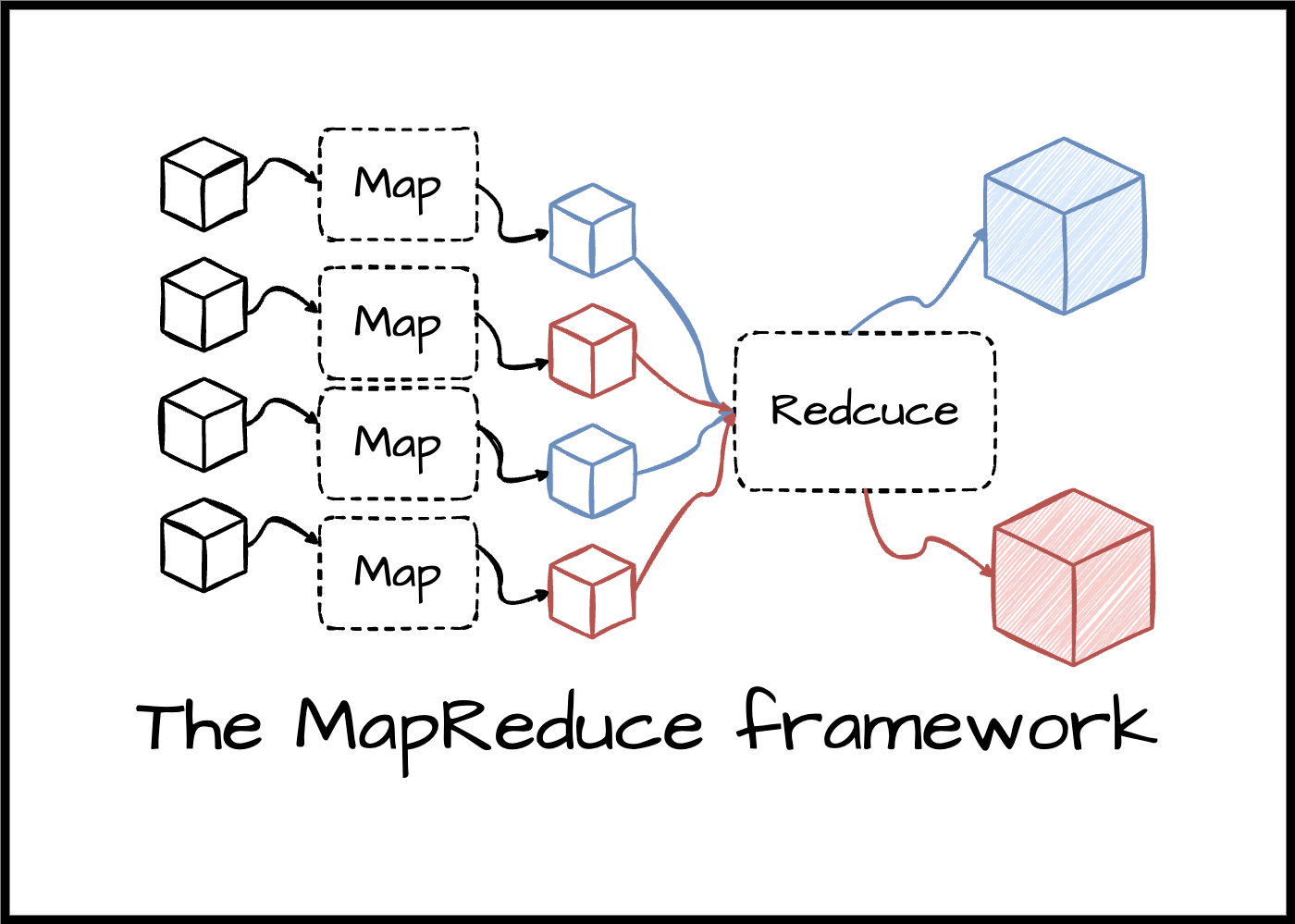
Big Data processing has a popular technique MapReduce. It’s helpful when you need to process a huge amount of data efficiently. It works in the following way:
- Split: Split the data in chunks (approximately of the same size)
- Map: Process the data in parallel
- Reduce: Combine the results into the final results
The same idea visualised:
To give an example, let’s find out what is the most popular word on, idk, let’s say, THE ENTIRE INTERNET. As you can imagine, this is quite a lot of data and processing the entire Internet webpage by webpage will take a while.
So the solution is to process webpages in parallel and then combine the results, as shown on the following picture.
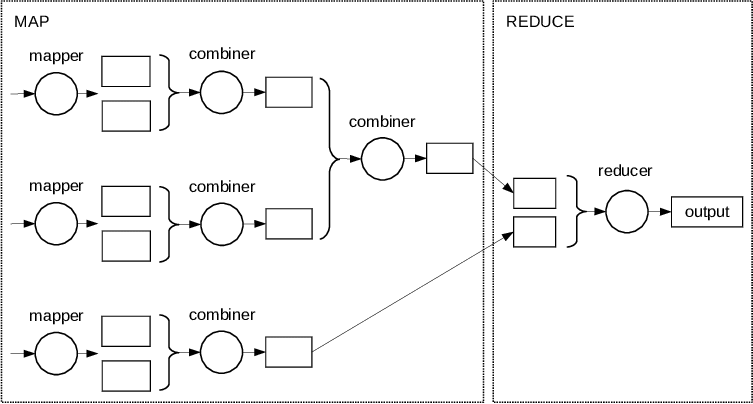
In practice, MapReduce pipelines are so massively parallel, a single reducer is not processing all the data at once. It process some chunks, ideally in parallel too, and when more data is available, more data can be combined.
This is where the associativity property comes into play.
If you have three expected results from the Map step
(let’s name them x, y and z), and
the first two are processed faster, you’ll get the final result in the
shape of:
combine (combine x y) zBut if y and z are ready earlier, you’ll
get this instead:
combine x (combine y z)As you can guess, you’ll get the same result only when the operation
combine is associative.
In other words, you don’t need to wait for all the results to finish! You can start combining the chunks earlier if the combiner is a Semigroup, thus, processing all the items faster.
Zero-cost abstractions?? Pff, how about Negative-cost abstractions that actually improve the performance after you use them!!
Commutativity
Associativity is great but it’s not strong enough for MapReduce.
If in our example we have x and z available
earlier, we still need to wait for y to finish before we
can combine. If all we know about combine is
associativity, we can’t just do the following:
(combine x z) yFor this, we need a stronger property commutativity.
This property was briefly mentioned in Part 1 of
this series. But to formalise it a bit, a binary operation is
commutative when the following property holds for all
values x and y:
x ⊕ y = y ⊕ xQuite a lot of real-world operations actually satisfy this property, so this seemingly stronger requirement is not a huge limitation for flows like MapReduce in practice.
🧑🔬 A Semigroup with a commutative binary operation is called Commutative Semigroup or Abelian Semigroup.
Conclusion
In this part, I explained why associativity truly matters. On a few practical examples I demonstrated the benefits of composable abstractions for correctness, extensibility and performance.
In the next part, we’ll explore how to implement polymorphic functions that work efficiently with every Semigroup (wat??).
If you liked this blog post, consider supporting my work on GitHub Sponsors, or following me on the Internet: